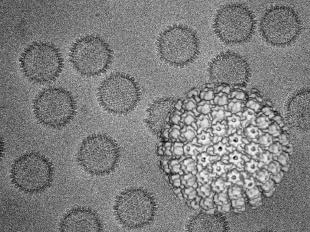
Watson and Crick are known for working out the helical structure of DNA, but when I was in grad school, I learned that they also thought deeply about the structure of viruses too. They made a prediction, by a real feat of imagination, that the teeniest, tiniest ball-shaped viruses should be icosahedrally symmetrical, kind of like the pattern on a soccer ball.
Today we're so accustomed to seeing beautiful images of viruses — there's a particularly infamous one that we've all seen on the news — that we take their unusual geometry for granted. Never did I hear anyone ask in all my years why a virus is typically drawn with facets, or flat sides, even vis-a-vis cells which are round and blobby.
Viruses, it turns out, form a nice little bridge between physics and biology. It may surprise the reader to learn that viruses are often so regular and symmetrical that they can form crystals, like salt does, or even liquid crystals like the display you're reading this on now.
In as early as 1935 they were centrifuging out mysterious proteins from the sap of tobacco plants infected by the tobacco mosaic virus. When precipitated out into a gel, the proteins formed a birefringent liquid, which happens when you have a liquid made from lots of tiny little rods. The mystery protein was the tobacco mosaic virus. This is how we learned that it was shaped like a long, thin cigarette.
In the same experiment, when they shined X-rays onto these liquid crystals, they saw hexagonal diffraction patterns. Somehow — and I don't entirely understand how — they correctly inferred that the little rods were made of smaller, and possibly triangular, subunits. It was crystals all the way down, apparently.
From what I can tell, during the 1930s and '40s, pretty much everyone who worked in physical virology was crystallizing plant viruses and publishing their diffraction patterns. Unfortunately diffraction patterns only give you a kind of abstract, kaleidoscopic representation of the real physical shape. To infer that, you either need a computer (which nobody had) or a lot of experience.
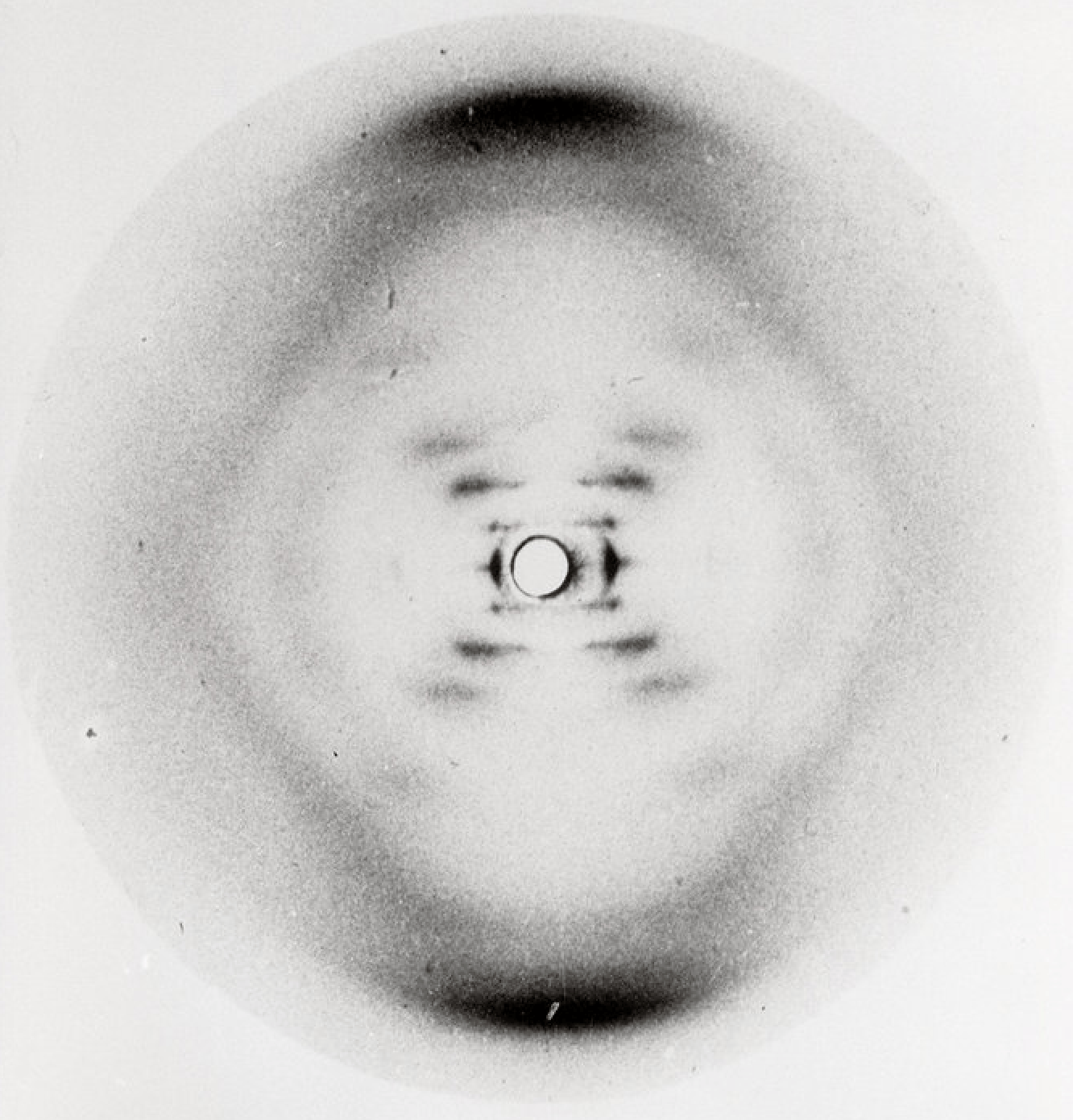
So by the early 1950s, people were starting to make educated guesses about what shapes these diffraction patterns of virus crystals actually implied. The sharpness of the diffraction patterns indicated that the crystallized viruses had nearly atom-for-atom identical shells, and the symmetry of those patterns indicated that they should be symmetrical too, but what shape were those shells, exactly? Dorothy Hodgkin, a Nobel prize winner in her own right, thought that since the lattices in her diffraction patterns were cubical, that the viruses must themselves be cubes, or at least have cubic symmetry, like an octahedron.
A reasonable guess, and wrong.
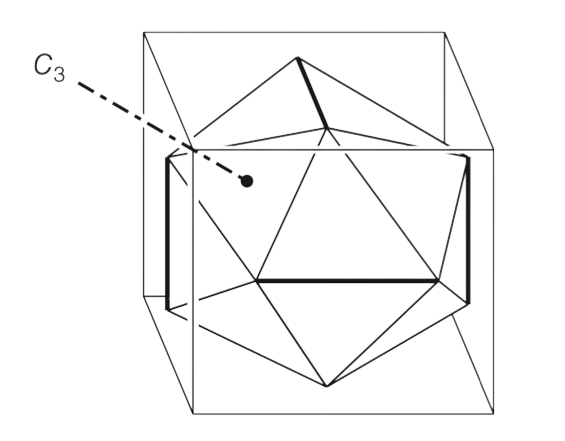
Watson and Crick knew the rather non-obvious fact that icosahedrons could also form a cubic lattice. (They were famous for playing with tinker toys and cardboard, and I wonder if this intuition had its roots there.) This detail, plus a few other papers that hinted at five-fold symmetry in X-ray diffraction patterns of crystalline virus, gave them a tailwind to publish in 1956 one of the coolest arguments I've ever heard, where they infer that viruses are probably icosahedrons, mostly as a result of the short length of their RNA.
They thought: given the tiny weight of the smallest viruses, and the fact that the RNA was known to make up only a small fraction of that weight, the total viral RNA could only be a few thousand base-pairs long — say, around 2000 — just enough to code for one protein. This is the crucial observation: instead of discovering that this or that virus must be made of lots of the same subunit, they deduced that it must be the case, purely from the weight of the RNA strand.
From this perspective, a virus just an RNA core plus a bunch of copies of the exact same protein put together in some nice way. The protein, logically, should form the shell that protects the comparatively fragile RNA.
But this raises a dilemma. Proteins don't usually neatly fit together to make a nice closed surface. They're like jigsaw puzzle pieces. How do you tile them over an RNA core to get a nice, compact, closed shape?
There are two main ways, they discovered: rods, and balls, depending on the shape of the puzzle piece. The key insight was that for the pieces to fit together, the local environment of each subunit must be the same as for every other subunit (for the rods, they ignored the endcaps if they exist.) It's a little easier to see that by reusing the same piece over and over you can construct a rod or even a helix. These are just those kinds of viruses that form liquid crystals, like the tobacco mosaic virus.
For the viruses that didn't form liquid crystals, the condition that every subunit lives in the same environment as every other one left only a handful of options for how these objects could be arranged: the Platonic solids. Notice how for these surfaces, every vertex and face is indistinguishable from all the others.
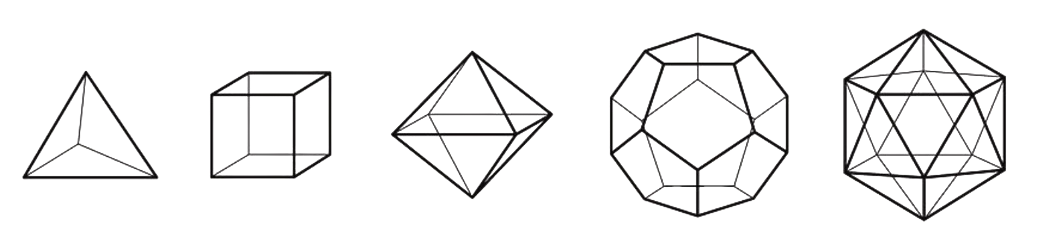
Looking at the different shapes, you can see that there is one that stands out as particularly likely to accommodate the RNA/proteins: the icosahedron (far right). Its relative roundness and large number of facets accommodates proteins which are the smallest compared to the overall size of the DNA. And this was the essential prediction of Watson and Crick, that viruses should have this insanely high degree of symmetry.
Five years later, images like this were published:
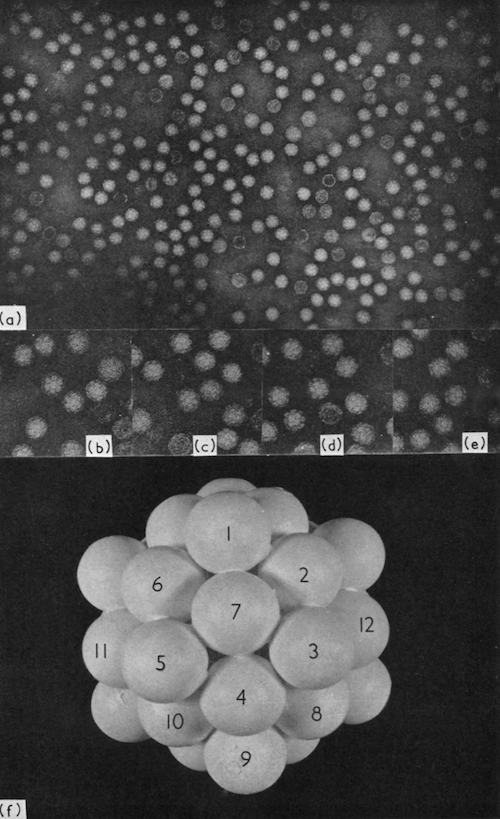
How Einsteinian to be able to predict such a thing: that the smallest organisms to exist should be crystalline, and icosahedral at that.
That the analogy to crystals was so compelling plays a large part in why I dropped out of my PhD.
I ended up working a mathematical model of virus formation that threw away the RNA, the proteins, everything. It was a gamble — had it worked, it would have been huge. My advisor's idea was to consider smooth, spherical shells that slowly deform into complex shapes, like (say) icosahedra, octahedra, or something else, as they cool. It was part of a program of applying an old but successful theory from the 1930s about particular kinds of matter-to-matter transitions to a new domain where the limits of the theory weren't known.
Well I spent about a year doing the calculations and learning all kinds of things about group theory, representation theory, spherical harmonics and all that. At the end, I could confidently say our model did reproduce the shapes we expected — along with every other shape you could possibly imagine, depending on the constants you picked! And since there was no way to know the "right" constants that gave us that icosahedral symmetry, we weren't predicting anything, and me and my advisor had a whole big blowout where I said it was this way and he said it was that way, and we couldn't find common ground.
Eventually I left, and I stand by that decision, but as far as I know he's still pursuing this.
In hindsight I think he was after some kind beautiful mathematical argument à la Watson and Crick, some other fundamental reason for why we see what we see. It's the kind of thing every physicist dreams of discovering. Who knows, maybe some day he'll find it.
Comments
Gabrielle: So you're telling me herpes is actually sacred geometry?